【人気ダウンロード！】 鋭角三角形 条件 290149

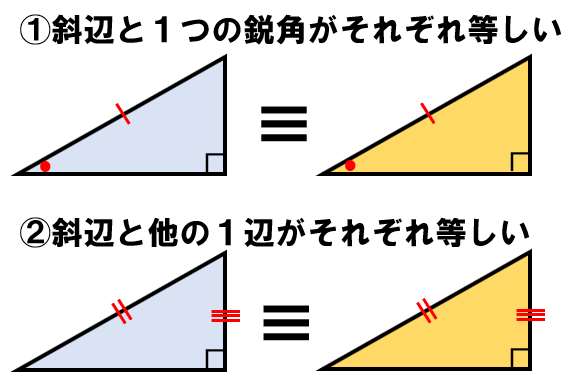
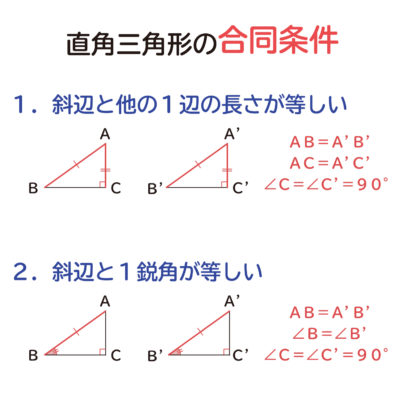
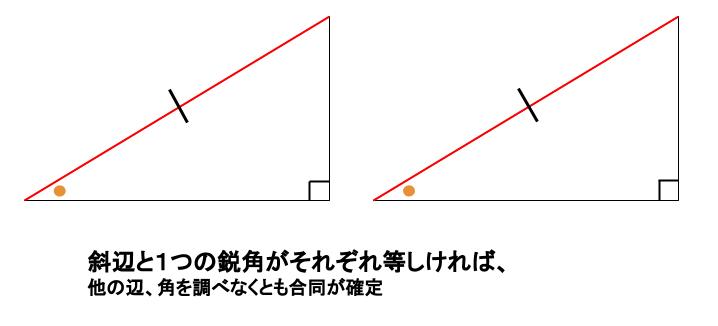
直角三角形の合同条件 直角三角形の合同条件 2つの直角三角形は、次の場合に合同である。 1 斜辺と1つの鋭角が、それぞれ等しいとき（証明） 2 斜辺と他の1辺が、それぞれ等しいとき（証明）数学・算数 数Iの三角形の成立条件の問題について 問題 a＝x、b＝2、c＝1の三角形ABCを考える （1）三角形ABCが存在するようなxの値の範囲を求めよ （2）三角形ABCが鋭角三角形とな 質三角形の合同条件は全部で5つです。 三角形の合同条件に加えて、直角三角形の合同条件を覚えるようにしましょう。 ・斜辺と1つの鋭角がそれぞれ等しい なお、日本では直角三角形の合同条件として「斜辺と1つの鋭角がそれぞれ等しい」も学びます。

B2c2a C2 X X2 Descubre Como Resolverlo En Qanda

鋭角三角形 条件

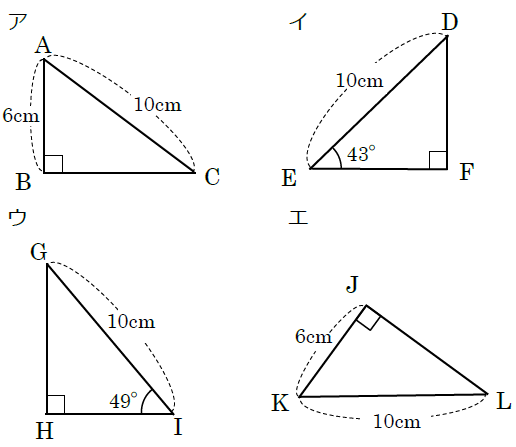
鋭角三角形 条件-よって 「2組の辺とその間の角がそれぞれ等しい」という条件にあてはまり合同といえる。 △ABCと△IGHは2組の辺が等しくなっているが、この2組の辺の間の角は等しいとわかっていないので 条件にあてはまらず、合同とは言えない。 例2\(\displaystyle \frac{a^2b^2c^2}{2ab}=0\)より 直角三角形の条件は\( a^2b^2=c^2\) であること。 これは三平方の定理から明らかですね。 鋭角三角形の条件 すべての角が90 より小さい 直角三角形の合同条件 を苦手にする人は多いですが，ぜひ挑戦してください。

鋭角三角形と鈍角三角形をみわける3つのステップ Qikeru 学びを楽しくわかりやすく

 三角形の形状の分かれ目 (その二) 数学 本記事では、三辺のうち二辺の長さが既知で残りの一辺の長さが未知である三角形の形状が鋭角三角形・直角三角形・鈍角三角形のいずれになるかについて考えます。 長さが既知である二辺のうち長い方をa、短い方相似条件 ある2つの三角形について、以下の条件のうち1つでも満たしていれば、その2つの三角形は相似である。 三辺比相等（三辺の比相等） 対応する3組の辺の長さの比が等しい直角三角形の合同条件 以下の 2 2 つを利用します。 1 斜辺と 1 1 つの鋭角がそれぞれ等しい。 この 2 2 つは暗記してください。 三角形の合同条件 3 3 つを暗記しましたね？ 同じことです、覚えないと話になりません。

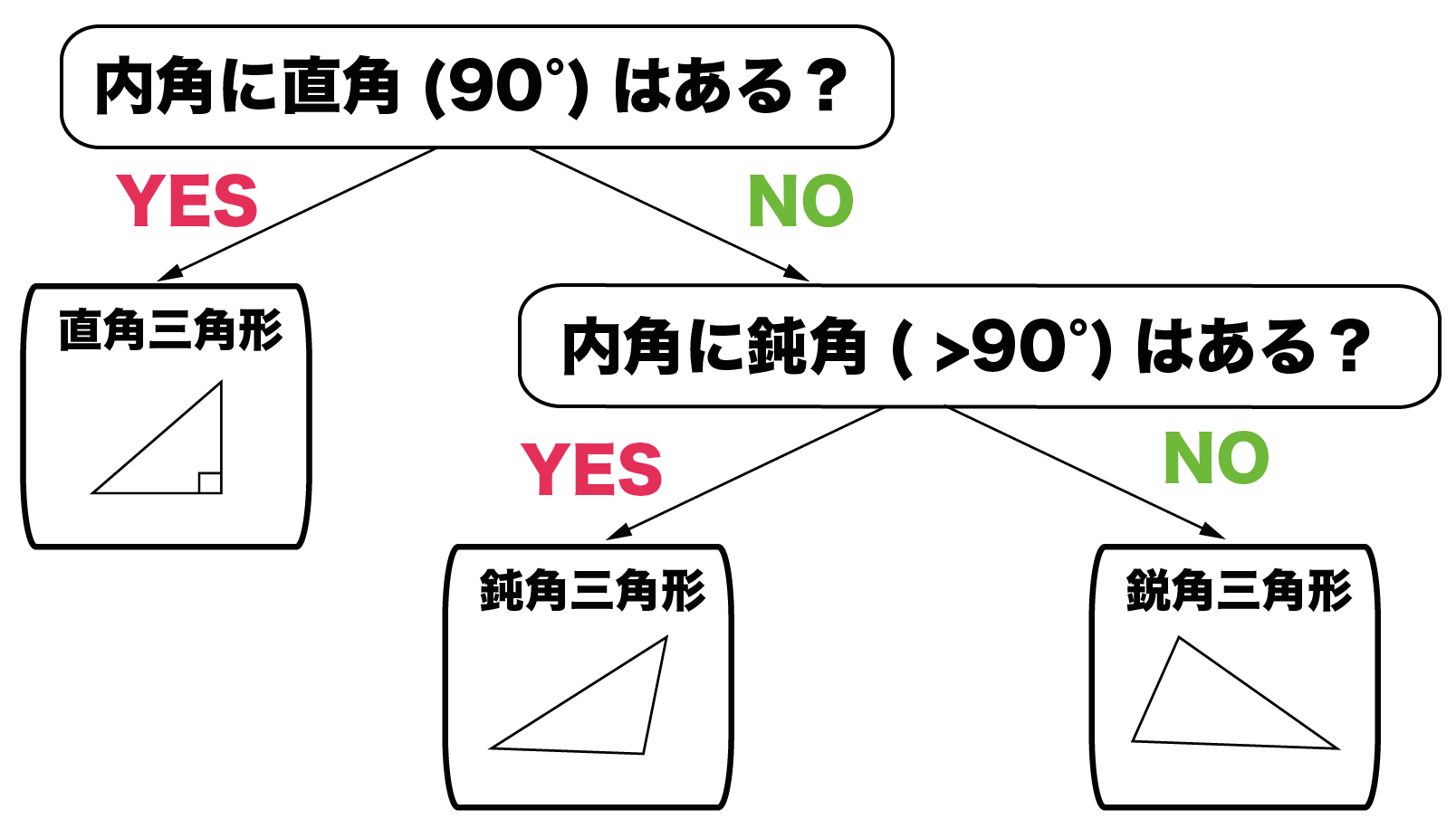
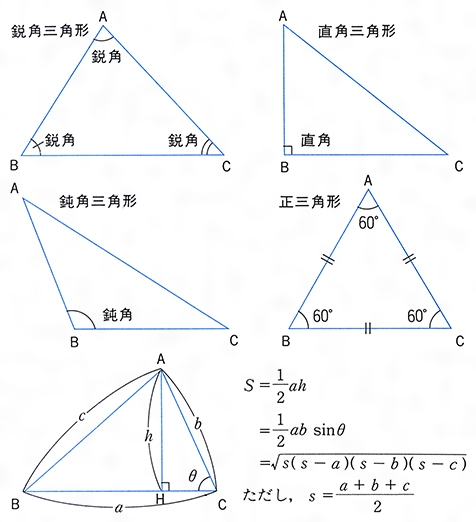
 すべての内角が 90° 90 ° 未満のとき， 鋭角三角形 と言います． 一つの内角がちょうど 90° 90 ° のとき， 直角三角形 と言います． 一つの内角が 90° 90 ° より大きいとき， 鈍角三角形 と言補足 三角形が1 つに定まる条件は，三角形の合同条件と一致する。 3 H さん：2の(3)について，もう少し詳しく調べてみましょう。 問題 2の(3)において，右の図のようにb を考え，b に関する b 方程式を作り，その解と三角形の関係を考察してみよう。 B a C A c b2542 直角三角形の合同条件 問題 1 2つの三角形の合同条件は何でしょうか？ 正解 ： 直角三角形の斜辺と他の1辺がそれぞれ等しい。 (RHS) 問題 2 2つの三角形の合同条件は何でしょうか？ 正解 ：直角三角形の斜辺と1つの鋭角がそれぞれ等しい。 (RHA)

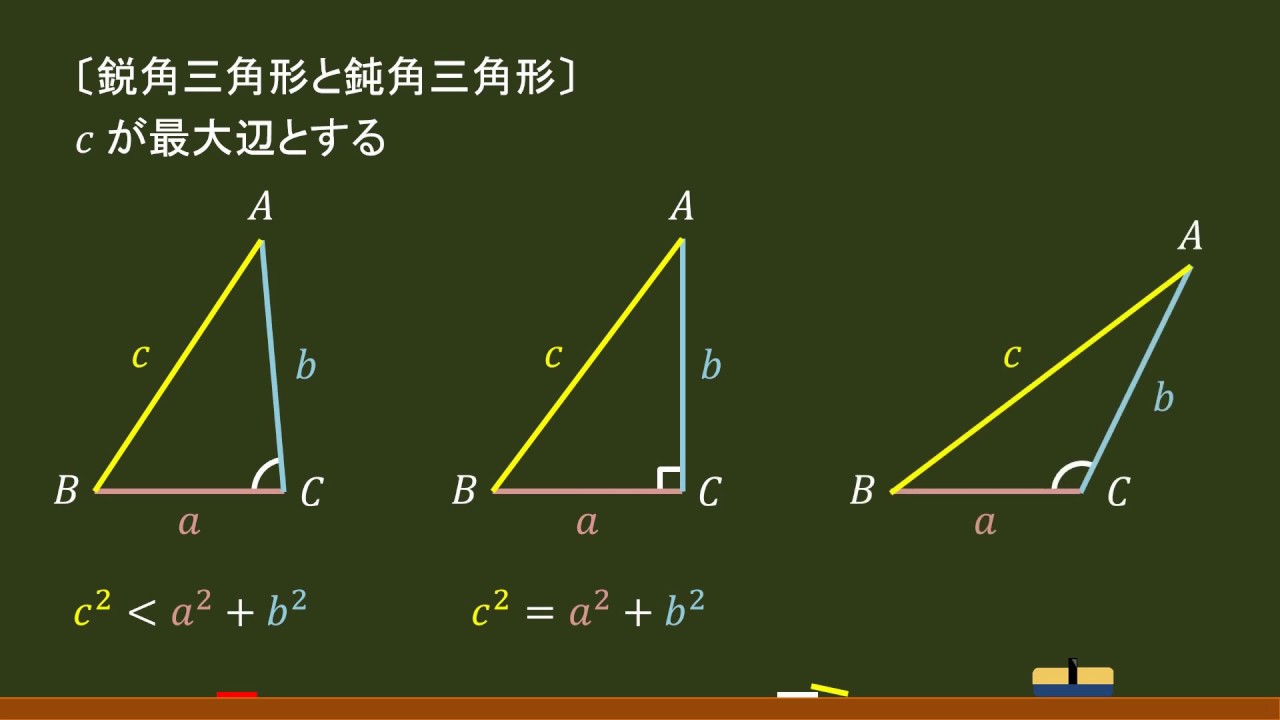
鋭角三角形（えいかくさんかっけい、英 acute‐angled triangle ）は、三角形の一種で、すべての角が直角 (90°=π/2 rad) よりも小さい図形である。 なお、鋭角三角形では、長辺をc、短辺をa,bとすれば、各辺は c 2 < a 2 b 2 の関係となり、また外心や垂心が三角形の内部に生ずる。 三角形の鋭角・直角・鈍角条件、三角形の成立条件3パターン 3辺の長さが$a=4,\ b=3,\ c=2$である$$ABCは鋭角三角形・直角三角形・鈍角三角 三角形の鋭角・直角・鈍角条件 最大辺が$a$であるから,\ その対角$A$が最大角である} すなわち,\ 角$A$が鋭角か直角か鈍角かでどの三角形かが決まる 3辺の長さから角度を求めるには余弦定理を用いる ある 結局,\ 余弦定理で求めた 〈直角三角形〉 ⑤斜辺と他の1辺がそれぞれ等しい（斜辺他一辺相等） ⑥斜辺と1つの鋭角がそれぞれ等しい （斜辺一鋭角相等） まず、「受験算数」において「三角形の合同条件」は頭に入れておく必要があるかどうかについてですが、これは「必要である

二等辺三角形であることの証明 二等辺三角形の定義性質 教遊者

高校数a 図形 鋭角三角形 鈍角三角形の判別方法 オンライン無料塾 ターンナップ Youtube

鋭角（えいかく）とは、0度より大きく90度より小さい角度のことです。 例えば45度、60度は鋭角です。 また90度より大きな角度を鈍角（どんかく）といいます。 1つの角度が90度の三角形を直角三角この問題の最大のポイントは「鋭角三角形をなす条件」です。 しかし、鋭角三角形をなす条件というのは、高校数学の教科書のどこにも明確に登場しません。つまり、知っている条件 三角形の合同条件 ①3辺相等 ②2辺夾角相等 ③2角夾辺相等 7 三角形 相似条件 三角形（さんかくけい、さんかっけい、拉 triangulum, 独 Dreieck, 英, 仏 triangle, (古風) trigon) は、同一直線上にない3点と、それらを結ぶ3つの線分か

中2数学 鋭角 鈍角とはいったい何ものなのか Qikeru 学びを楽しくわかりやすく

直角三角形の合同条件 算数 数学が好きになりmath

鋭角三角形ABC の時↓図、 （どの頂点も90°より小） 外心Oは ABCの内部 にある。 直角三角形ABCの時↓図 外心Oは斜辺の中点 にある。 鈍角三角形ABCの時↓図 （90°より大の角を持つ） 外心Oは鈍角の対応する 辺（下図では辺BC）の三角形（さんかくけい、さんかっけい、拉 triangulum, 独 Dreieck, 英, 仏 triangle, (古風) trigon) は、同一直線上にない3点と、それらを結ぶ3つの線分からなる多角形。 その3点を三角形の頂点、3つの線分を三角形の辺という。直角三角形の合同条件に出てくる 「鋭角」 というのは、 90°より小さな角 のことだよ。 ここでは、簡単に言うと 「直角でない2つの角のうちの1つ」 を指すよ。 ちなみに、 90°よりも大きな角 のことを 「鈍角」 というんだ。

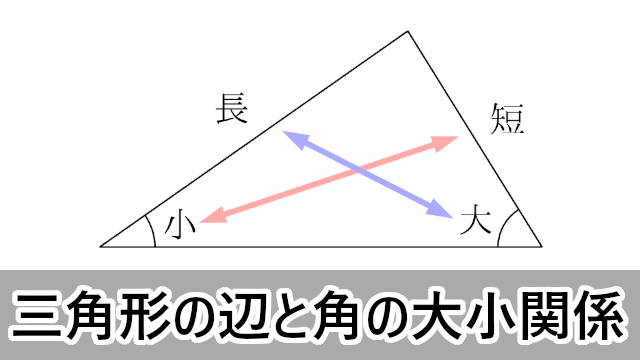
数学ia 三角形の角の大きさと辺の長さの関係 大学入試数学の考え方と解法

直角三角形 Wikipedia

 z を複素数とする。複素数平面上の3点 A ( 1 ) , B ( z ) , C ( z2 ) が鋭角三角形をなすような z の範囲を求め、図示せよ。16 東京大・理イズミの解答への道 複素数平面で問題は与えられているが、三角関数基本形の条件 式 し、 3辺の長さa,b,cを与えると、三角形が構成可能な場合は、 直角三角形ならば白、鋭角三角形ならば青、鈍角三角形ならば赤色で、亀場に描くプログラムを作成しなさい。 また、もし三角形が構成できない場合は、"no such triangle" と亀場三角形の成立条件とその証明 レベル ★ 基礎 平面図形 更新日時 三角形の成立条件（存在条件）：三辺の長さが a, b, c a,\b,\c a, b, c である三角形が存在する必要十分条件は， a b > c ab > c a b > c かつ

中学2年の数学 動画 鋭角三角形と鈍角三角形の問題 19ch

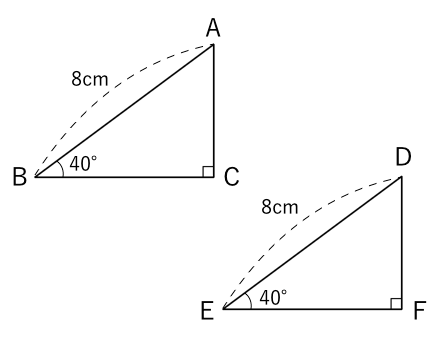
直角三角形の合同 条件 について 苦手な数学を簡単に

三角形（さんかくけい、さんかっけい、拉 triangulum, 独 Dreieck, 英, 仏 triangle, (古風) trigon) は、同一直線上にない3点と、それらを結ぶ3つの線分からなる多角形。 その3点を三角形の頂点、3つの線分を三角形の辺という。 この2条件を両方満たしていれば、鋭角かどうかはともかく、三角形になります。 ただし、この問題に関しては、点Pと点Qが原点対称で、点Rがx軸上にあることから、3点が三角形をなす条件が簡単にまとめられます。 ・上の条件（どの2点を選んでも同一の点ではない条件）は、 （x，y）が原点ではない かつ （1，0）ではない かつ （－1，0）ではない。 ・下の条件（3ゆえに、鋭角三角形と鈍角三角形の出来る確率は等しい。 逆は必ずしも真ならずですが、今度はこれでいいような気がします。 如何なものでしょうか。 ところで、直角三角形は、鋭角三角形と鈍角三角形のどちらに含まれるのでしょうか。

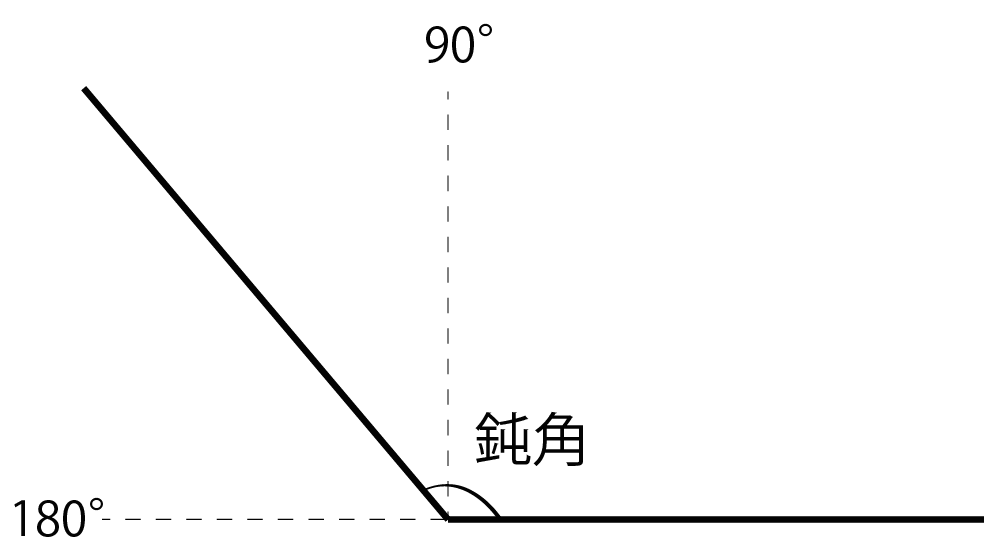
中2数学 鋭角 鈍角とはいったい何ものなのか Qikeru 学びを楽しくわかりやすく

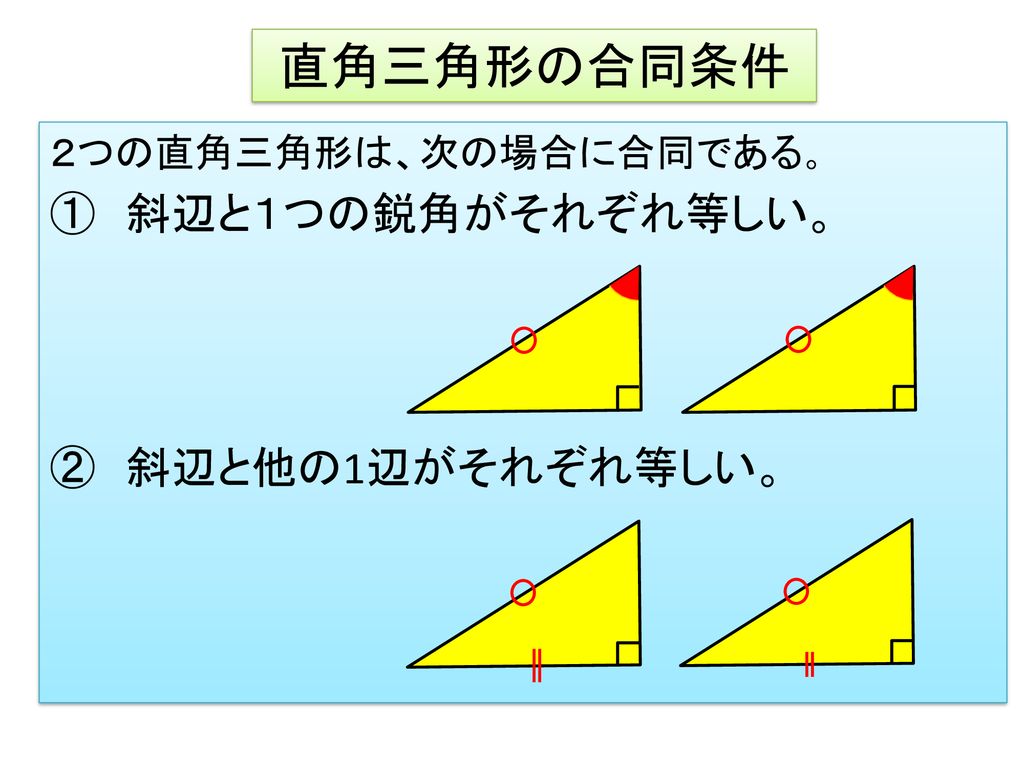
本時のねらい 直角三角形の合同条件を導き それを理解し 証明ができるようにする Ppt Download

鋭角三角形となるための条件について，一般的に 確認しておきましょう． 辺の長さに注目 3 辺a,b,c に対し 2a b2 > c2 b2 c2 > a2 2c a2 > b2 の全てが成り立つことが条件です．a ≤ b ≤ c と条件 をつけておけば，c が最大なので，下2 つの不等式

2 60第４章 直角三角形 直角三角形の合同条件 Kakera Link 公式ブログ

鋭角三角形と鈍角三角形をみわける3つのステップ Qikeru 学びを楽しくわかりやすく

三角形の成立条件と鋭角 直角 鈍角三角形の判定 数学の偏差値を上げて合格を目指す

数i 必要十分条件の判別 鋭角三角形など Youtube

中２数学 鋭角三角形 鈍角三角形 直角三角形とは 小学生 中学生の勉強

中２数学 直角三角形の合同条件と証明問題 授業わかるーの Byナオドット先生 中学数学のわかりやすい解説サイト

48s96ub7b0z5f Net Sankakuhi Seiritsujouken Katachi

A ９０ は Abcが鋭角三角形であるための必要条件である Yahoo 知恵袋

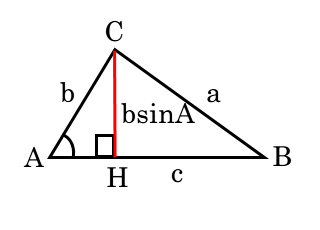
図形と計量 三角形の面積について 日々是鍛錬 ひびこれたんれん

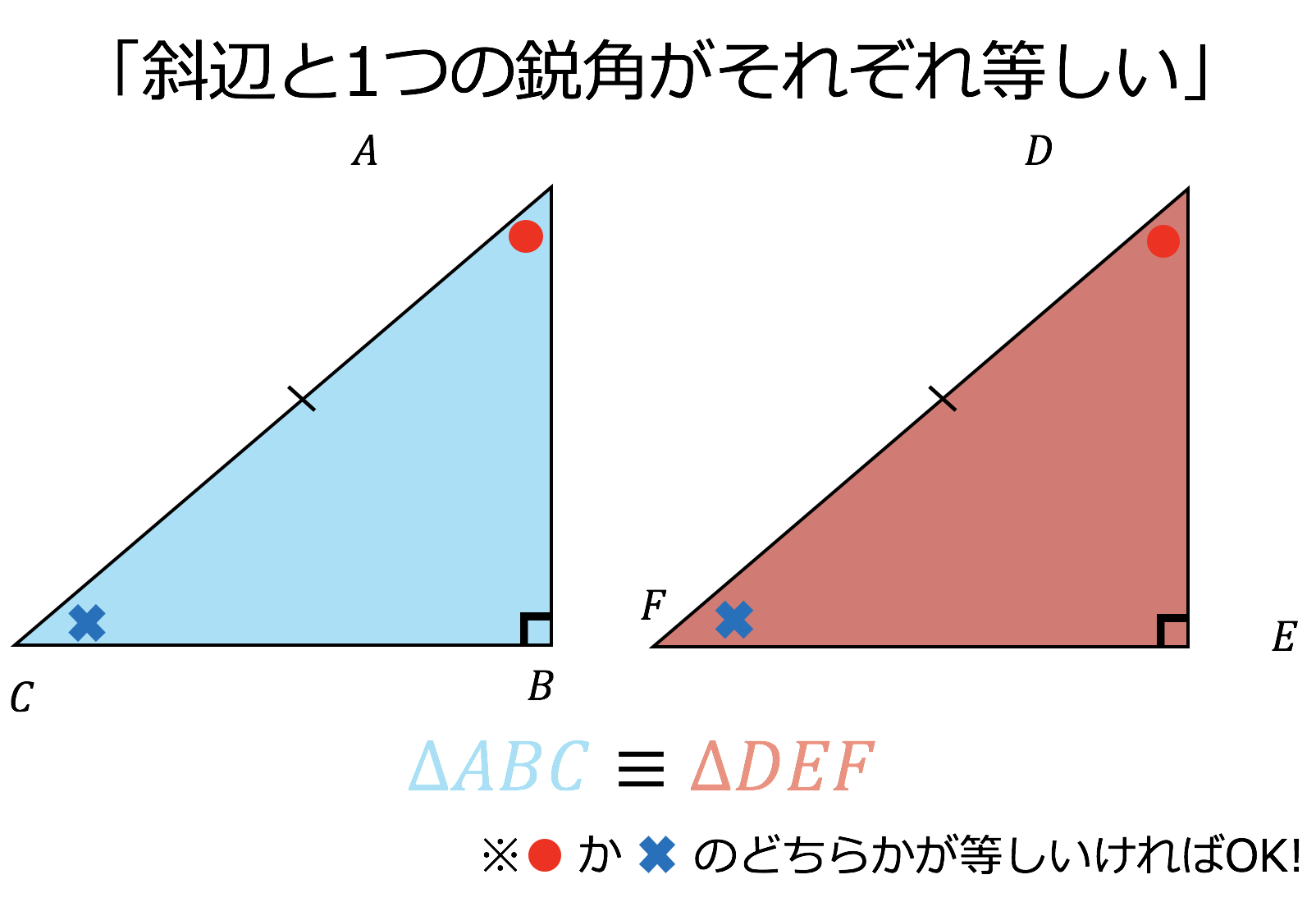
3分で分かる 三角形 直角三角形の合同条件とその使い方をわかりやすく 合格サプリ

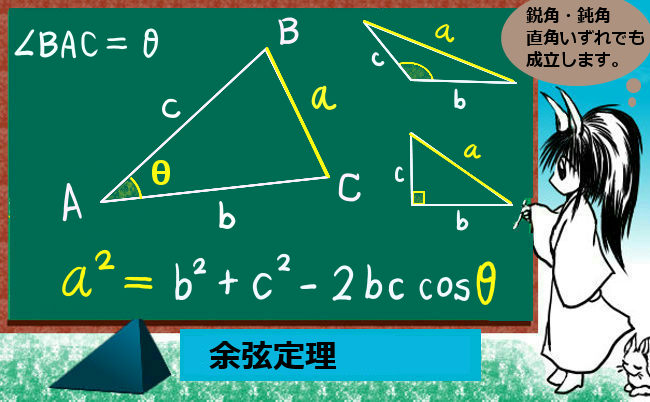
余弦定理 理数系無料オンライン学習 Kori

図形と計量 三角比の拡張について 日々是鍛錬 ひびこれたんれん

高校数学を初めから丁寧にvol 077 数学i 三角関数 鋭角三角形 鈍角三角形の判定 Youtube

東京大学 文系 理系 数学 図形 鋭角三角形 複素数平面 難関大学 数学の発想のしかた さくら教育研究所 Skredu

中２数学 鋭角三角形 鈍角三角形 直角三角形とは 小学生 中学生の勉強

直角三角形の辺の長さ 合同条件 面積について アタリマエ

なぜ鈍角三角形の成立条件の符号の向きがこの問題ではこうなのですか Clear

中２数学 鋭角三角形 鈍角三角形 直角三角形とは 小学生 中学生の勉強

考え方が分かりません Clear

1

三角形の存在条件 Pukiwiki

鋭角のときの 三角比の公式の証明 数学i By Okボーイ マナペディア

中２数学 鋭角三角形 鈍角三角形 直角三角形とは 小学生 中学生の勉強

直角 三角形 の 相似 条件

２０１６年 東大数学 理系第４問 三角形をなす条件 鋭角三角形の条件 複素数平面 オンライン受講 東大に 完全 特化 東大合格 敬天塾

高校数学a 正多角形内の三角形の個数 二等辺三角形 正三角形 直角三角形 鈍角三角形 鋭角三角形他 受験の月

鋭角三角形と鈍角三角形をみわける3つのステップ Qikeru 学びを楽しくわかりやすく

高校数学 数 ９２ 三角形となる条件 Youtube

数学ia 三角形の成立条件 大学入試数学の考え方と解法

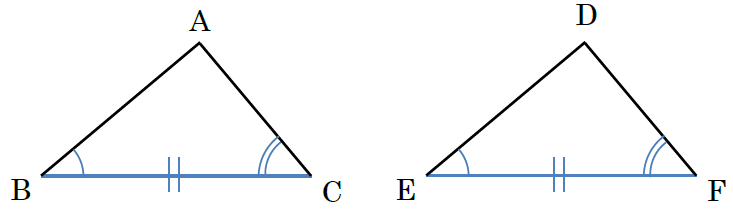
中２数学 三角形 直角三角形の合同条件の覚え方のポイントを解説 まなビタミン

1

B2c2a C2 X X2 Descubre Como Resolverlo En Qanda

直角三角形の合同条件 On Vimeo

２０１６年 東大数学 理系第４問 三角形をなす条件 鋭角三角形の条件 複素数平面 オンライン受講 東大に 完全 特化 東大合格 敬天塾

平行四辺形の対辺の長さは等しくなる ことの説明 おかわりドリル

高校数学a 三角形の重心 外心 垂心の位置関係 オイラー線 の幾何的証明 受験の月

鋭角三角形と鈍角三角形をみわける3つのステップ Qikeru 学びを楽しくわかりやすく

直角三角形の合同条件再び 中学校２年生の数学 身勝手な主張

直角三角形の合同条件 数学が嫌いなんです

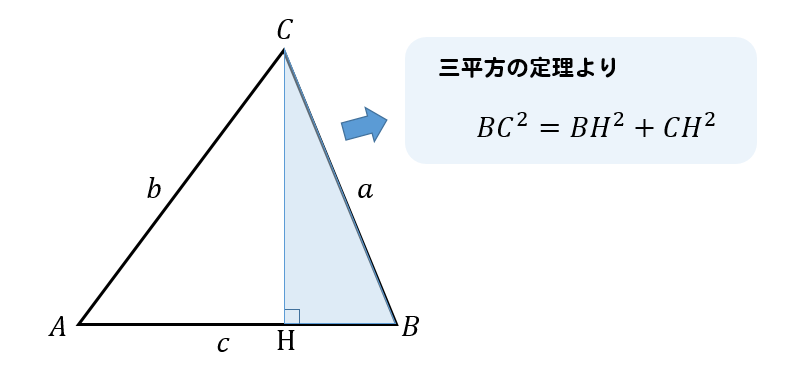
余弦定理の証明 簡単にわかりやすく考えてみよう 数スタ

鋭角とは 1分でわかる意味 定義と求め方 0度 範囲 鈍角との違い

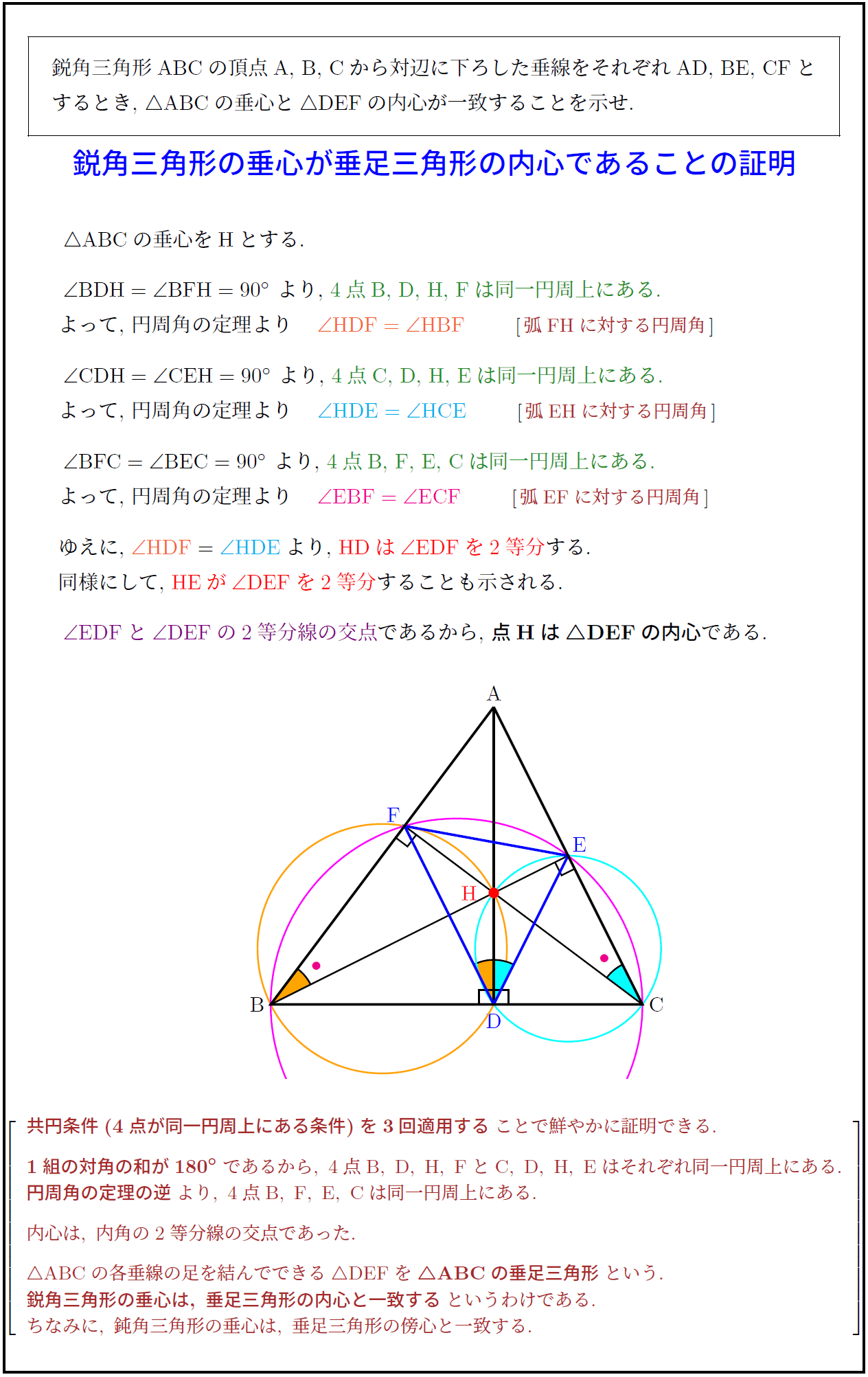
高校数学a 鋭角三角形の垂心が垂足三角形の内心であることの証明 受験の月

鋭角三角形 Wikipedia

直角三角形とは 定義や定理 辺の長さの比 合同条件 受験辞典

三角形の外心

鋭角三角形と鈍角三角形をみわける3つのステップ Qikeru 学びを楽しくわかりやすく

鋭角三角形と鈍角三角形の意味と見分け方 具体例で学ぶ数学

3分なるほど 三角形の内角 外角の性質について解説 数スタ

直角二等辺三角形 Wikipedia

鋭角の三角比とは 1分でわかる意味 辺の長さと角度の関係 三平方の定理

鋭角三角形と鈍角三角形をみわける3つのステップ Qikeru 学びを楽しくわかりやすく

二等辺三角形 直角三角形の定義 合同条件と証明問題 リョースケ大学

鋭角三角形 直角三角形 鈍角三角形かを調べる方法 数学i By ふぇるまー マナペディア

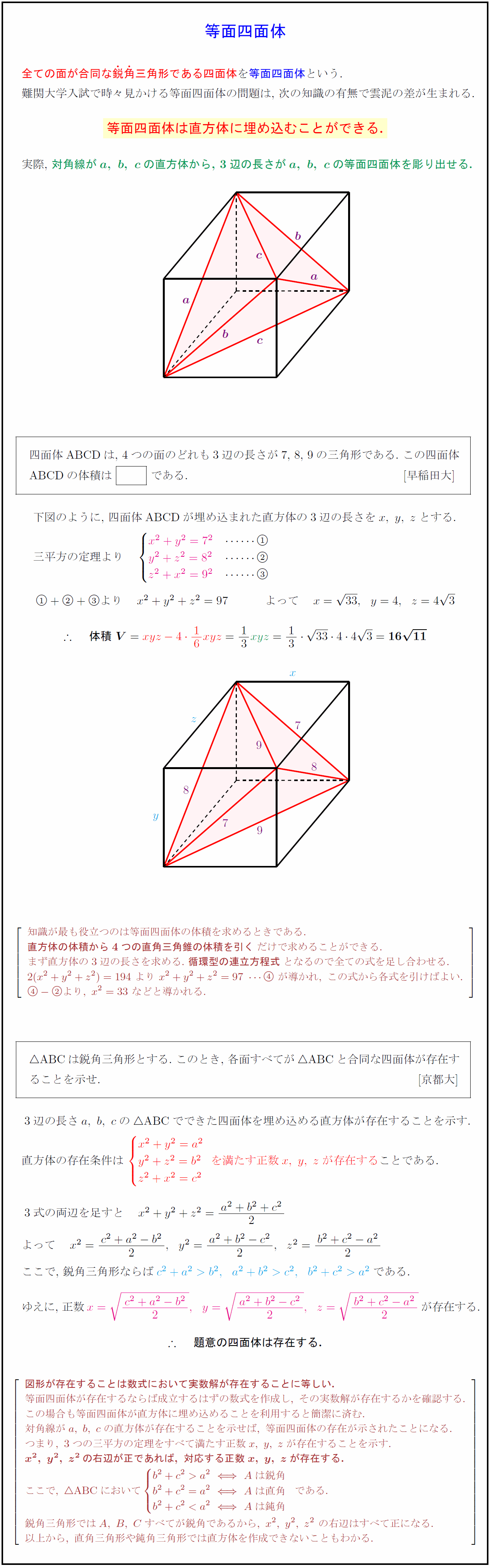
高校数学 等面四面体の体積と直方体への埋め込みと存在証明 受験の月

Basicプログラミング

鈍角三角形 鋭角三角形 直角三角形の違いを詳しく教えてください お願いします Clear

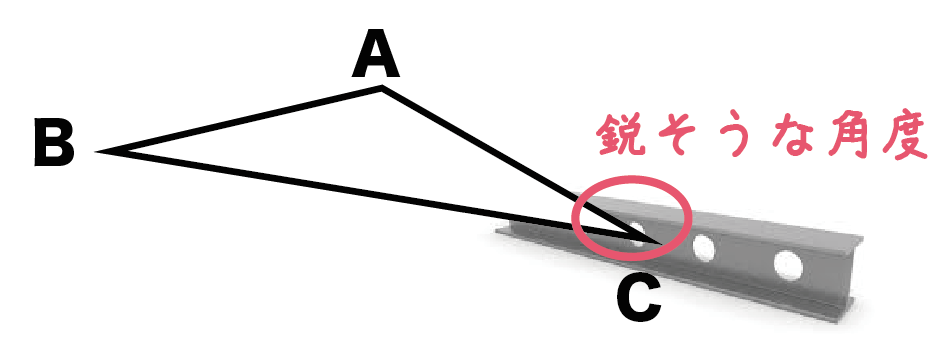
中2数学 鋭角 鈍角とはいったい何ものなのか Qikeru 学びを楽しくわかりやすく

直角三角形の合同条件とそれを利用した証明 チーム エン

二等辺三角形であることの証明 二等辺三角形の定義性質 教遊者

高校入試 英語 数学 学習 三角形と四角形 直角三角形

鋭角三角形と鈍角三角形をみわける3つのステップ Qikeru 学びを楽しくわかりやすく

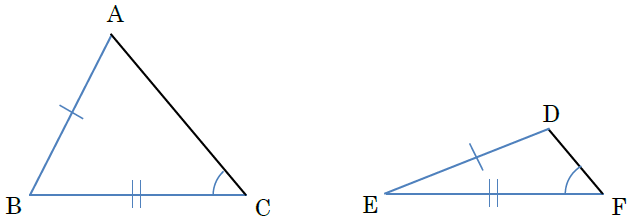
中２数学 三角形 直角三角形の合同条件の覚え方のポイントを解説 まなビタミン

鈍角 三角形 条件 鈍角三角形が存在する条件 Govotebot Rga Com

鋭角三角形とは 1分でわかる意味 条件 直角三角形 鈍角三角形との違い

直角 鋭角 鈍角三角形の判定法 思考力を鍛える数学

無料 中２数学 テスト対策 解答プリント 214 図形と合同２ 三角形の合同

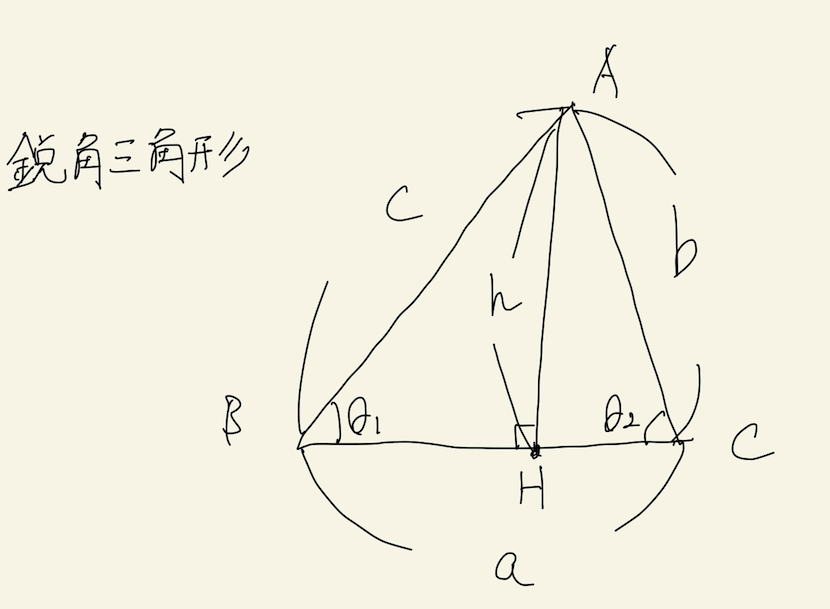
任意の三角形の垂線とその足による内分点の性質 物理u数学の友 質問 悩みに回答します

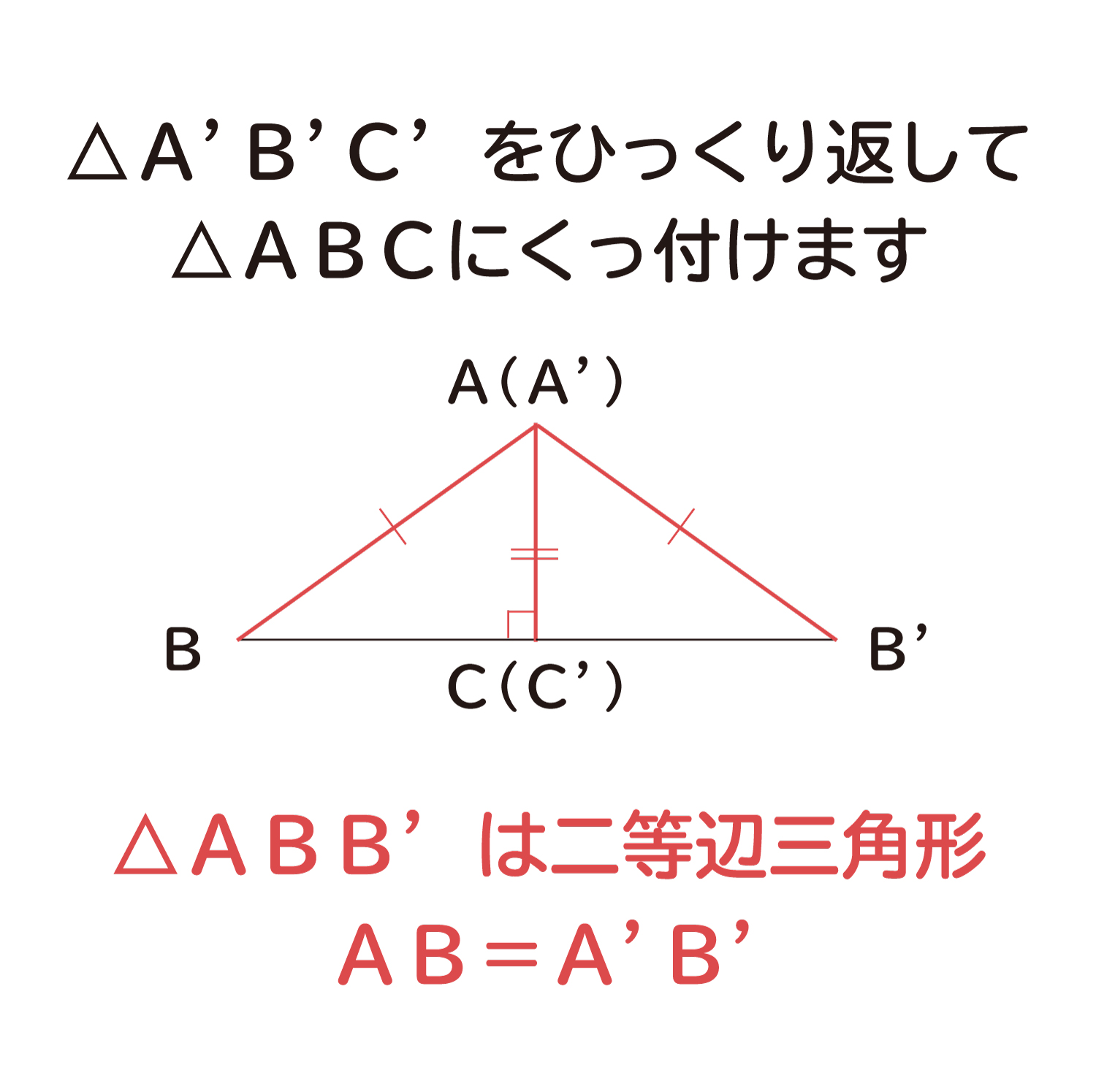
直角三角形の合同条件の説明 おかわりドリル

中２数学 三角形 直角三角形の合同条件の覚え方のポイントを解説 まなビタミン

3

鈍角 三角形 基本 鈍角の三角比 Docstest Mcna Net

直角三角形の合同条件

中２数学 鋭角三角形 鈍角三角形 直角三角形とは 小学生 中学生の勉強

２０１６年 東大文系数学 第１問 三角形の成立条件 鋭角三角形の条件 領域図示 オンライン受講 東大に 完全 特化 東大合格 敬天塾

中２数学 三角形 直角三角形の合同条件の覚え方のポイントを解説 まなビタミン

中学数学 直角三角形の合同条件 中学数学の無料オンライン学習サイトchu Su

鋭角三角形とは 1分でわかる意味 条件 直角三角形 鈍角三角形との違い

三角形とは コトバンク

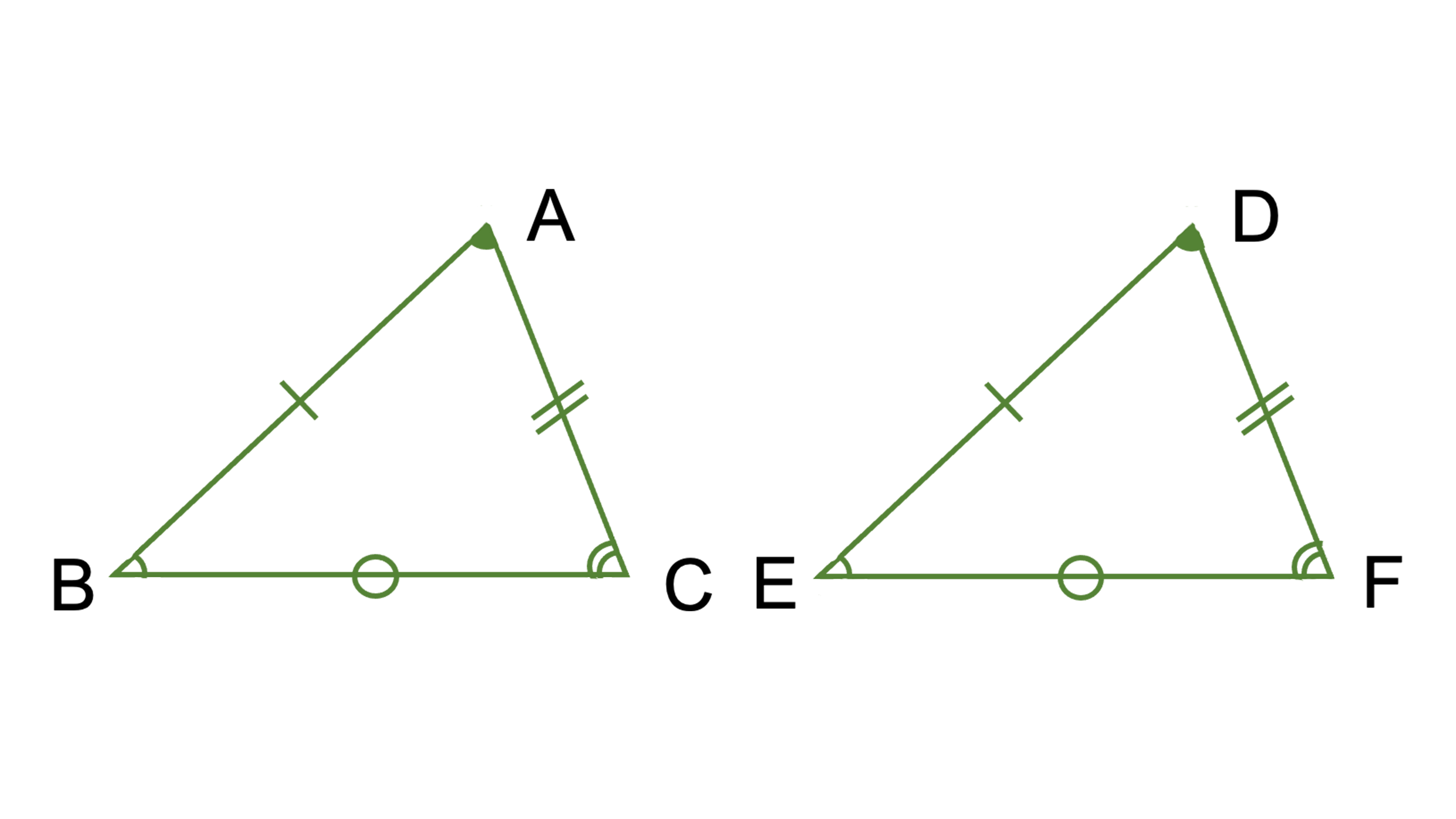
三角形の 合同条件 とは 直角三角形の2つも覚えて証明問題を攻略しよう お役立ち情報ページ 個別指導の学習塾なら個別指導塾スタンダード

𝐏𝐮𝐫𝐨 𝐒𝐡𝐨𝐝𝐚𝐢 Abcが鋭角三角形 Ab 2 2 Ac 2 2 Ac 2 Ab 2 Ac 2 Ab 2 2 今回は辺の長さの条件で処理した 別解 Abcが鋭角三角形 Bac P 2 Abc P 2 a P 2 これらを偏角の条件として表す 略 T Co

3分で分かる 三角形 直角三角形の合同条件とその使い方をわかりやすく 合格サプリ

鋭角三角形の三辺の中点を図のように結ぶと全ての三角形 Amr M Yahoo 知恵袋

直角三角形の合同条件とその証明 数学fun

直角三角形の合同条件を教えてください Clear

鋭角三角形

高校数学 三角形の鋭角 直角 鈍角条件 三角形の成立条件3パターン 受験の月

直角三角形の合同条件を使った証明とは なぜ2つ増えるのか 遊ぶ数学

1

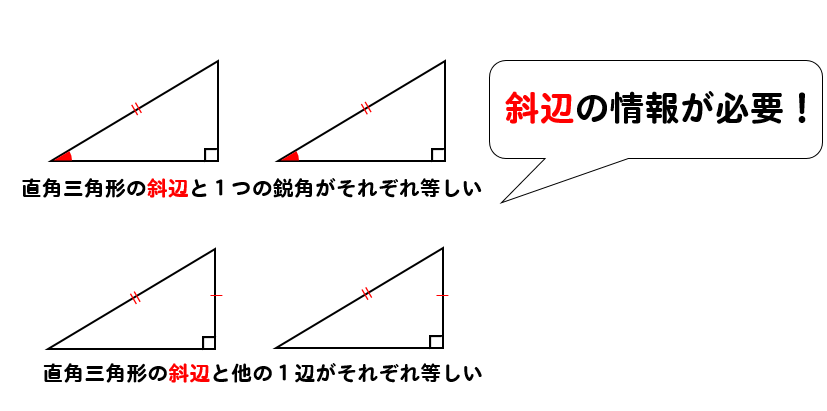
直角三角形の合同条件 証明問題の書き方とは イチから徹底解説 数スタ

外接円 外心について

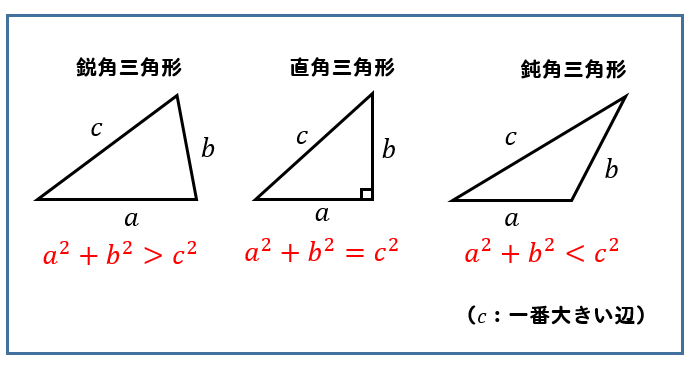
鋭角 鈍角三角形 三平方の定理を使って見分ける方法を解説 数スタ

数学 中2 50 鋭角三角形と鈍角三角形 Youtube

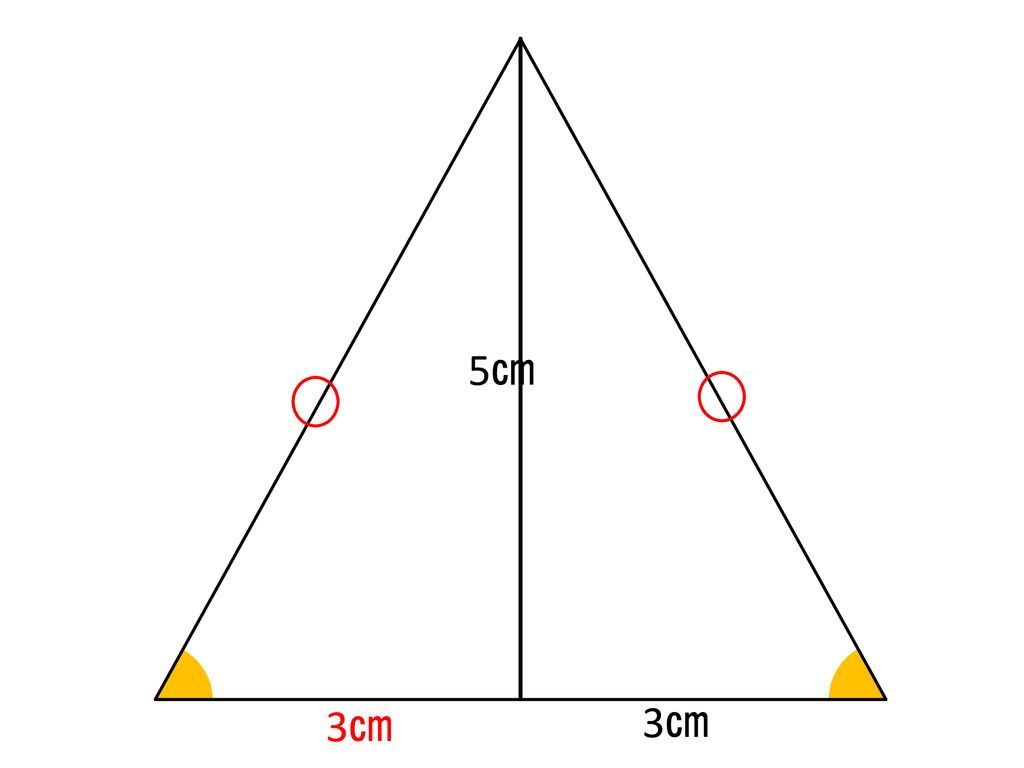
本時のねらい 直角三角形の合同条件を導き それを理解し 証明ができるようにする Ppt Download

誤答から学ぼうシリーズ 余弦定理を用いて三角形を解く ほのぼの数学頑張ろう